代表値の定義
代表値とは、データの分布全体の特徴を1つの数値で代表して表したもの、つまり、測定値の分布の中心的傾向を示す値です。
代表値には「平均値」「中央値」「最頻値」があります。
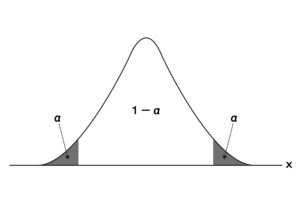
正規分布の場合に用いられるのが平均値です。
平均値は、データの総和をデータの数で割ったもので、大別して、算術平均と幾何平均と調和平均に分けられます。
正規分布から著しくはずれたデータの場合には、より頑健、つまり、分布の非対称性や外れ値の影響を受けにくい値を用いる必要が出てきます。
その場合に用いられるのが「中央値」や「最頻値」です。
中央値は、データ全体を大きさ順に並べたときに中央にくる値のことで、度数分布を左右均等に二分する値です。
順序尺度や間隔尺度、比率尺度で極端な値がある場合や、左右非対称な分布において用いられます。
最頻値は、度数の最も多く現れたデータの値のことであり、4つの尺度すべてで用いることができます。
ただし、階級の大きさや数によって非常に影響を受けやすいということに注意すべきでしょう。
代表値の関連キーワード
- 平均値
- 中央値
- 最頻値
- 散布度
代表値の補足ポイント
平均値は、算術平均・幾何平均・調和平均に大別されますが、これらについて、簡単に違いを確認しておきましょう。
いわゆる「平均をとる」といった場合に、多くの場合、用いられているのが「算術平均」です。
算術平均は、間隔尺度や比率尺度における左右対称な分布で、すべての測定値を考慮するときに用いられます。
ただし、データによっては「幾何平均」と「調和平均」を用いる方が妥当な場合があります。
具体的には、大きな値の影響を受けて分布の中心がずれるといった非対称な分布などの場合です。
こうした場合、例えば対数をとると少し左右対称に近づくとされます。
対数の平均を指数変換で戻したものを「幾何平均」と言い、変化率・成長率などの平均を求める場合には、これを利用するのが好ましいとされています。
対数をとっても足りないときには、逆数をとると左右対称にさらに近づくとされます。
そのために算出された、逆数の平均の逆数を「調和平均」と言います。
幾何平均と調和平均は、算術平均よりもデータの中央付近による、つまり、中央値に近い値となることが確かめられています。
さて、代表値として有名なのは、ここまでに挙げた平均値・中央値・最頻値ですが、広い意味で分布を代表する値として考えた場合には、散布度も含まれることがあるでしょう。
散布度は、統計データの散らばりの程度を表す数値です。
データの「範囲」「分散」「平均偏差」「標準偏差」などがあります。
代表値と散布度は共に、分布の特性を1つの値で表わすものですが、代表値が等しくても、その周りの分布の様子が同じとは限りません。
そのことを頭におき、データを分析・解釈する必要があると言えますね。
編集中