t検定

t検定の定義

t検定は、検定統計量の標本分布がt分布に従うという前提で実施される、統計的検定の総称です。
t検定には平均や相関係数、回帰係数の検定などのさまざまな種類が含まれますが、心理学では、2つの群の平均値の差を比較する際に使用される検定としてよく知られています。

ここでは、独立な（対応のない）2群の平均値の差に関する検定について説明していきます。
独立な2群とは、ある母集団から2群の標本を抽出したときに、標本内の対象が互いに無関係であることを意味します。

 
2群の平均値の差を比較するにあたって、帰無仮説として「2群の母平均に差がない」、対立仮説として「2群の母平均に差がある」という仮説を立て、データに基づいてこの仮説を検証していきます。

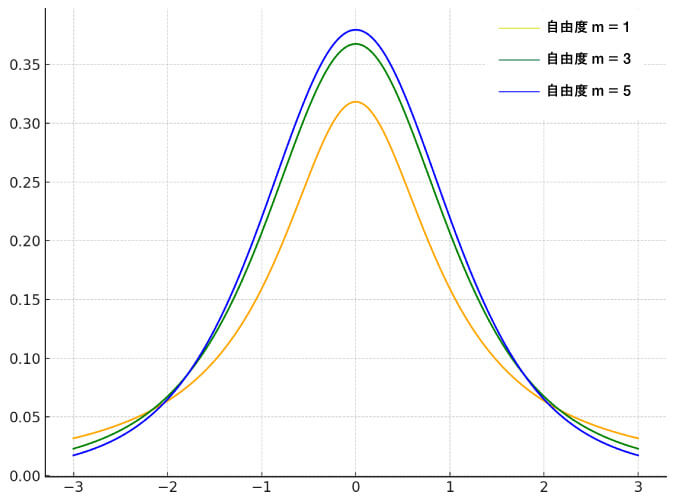
t検定を実施する際の前提となる標本分布であるt分布は、正規分布と同様に対称的な釣り鐘型をしています。
t分布は自由度（サンプルサイズ）によって形状が変化し、自由度が大きくなるほど正規分布に近づいていきます。

t検定は母集団が正規分布に従うと仮定して実施しますが、実際には母集団は未知であることが多いものです。
なぜなら、「日本人大学生の自尊感情について」調査する場合に、日本人の大学生全員に調査をすることはほぼ不可能だからです。

そこで、t検定では調査対象としたい母集団の一部（標本）から得られた標本分散を用いて推定を行い、正規分布の代わりにt分布を使用します。
母集団の標準偏差が未知の場合、特にサンプルサイズが小さい場合、t分布を使用することで、推定の不確実性を考慮でき、統計解析の信頼性を担保できます。

また、独立した2群のt検定では、調査対象を研究仮説に基づいて実験群と対照群（統制群）に分け、両者のデータを比較します。
この比較により、2群の平均値に統計的に有意な差があるかどうかを検証し、帰無仮説（差がない）を棄却できるかを判断します。

t検定の補足ポイント

t検定は、独立変数が質的変数、従属変数が量的変数の場合に適用されます。
性別（独立変数）と数学の試験の得点（従属変数）や、母親の飲酒習慣の有無（独立変数）と子どもの出生時体重（従属変数）などの検討に使用できます。

例えば、お菓子の製造業者について、その会社のSNSの投稿量（1日に5件以上または5件未満の投稿）の違いが、製品の売上高に影響を与えるかどうかを調査することができます。

この場合、独立変数はSNSの投稿量、従属変数は製品の売上高です。
なお、独立変数は「投稿量」と言っても、1日何件投稿しているかという量的変数ではなく､1日に5件以上投稿しているかそうではないか､という2択の質的変数になっています。

帰無仮説は、SNSの投稿量が多くても少なくても「2つの母平均は等しい」、つまり「製品の売上に差はない」となります。
そして対立仮説は「2つの母平均は等しくない」、つまり「製品の売上に差がある」です。

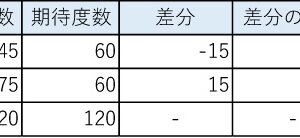
数式などはここでは割愛しますが、帰無仮説と対立仮説を設定したら、t値という検定統計量を算出します。
t値は、2つのグループの平均値の差を、差の標準誤差で割ることで求められます。

また、有意水準を決めておくことも忘れてはなりません。
心理学では5%、すなわちα=0.05とするのが一般的です。

そして、データから実際に計算されたt値（実現値、または観測されたt値）を求めます。
自由度と有意水準から、t分布表や統計ソフトウェアを用いて棄却域（臨界値）を調べます。

上記の実現値が棄却域に含まれていれば、有意水準5%で帰無仮説を棄却し、「SNSの投稿量の違いによって、製品の売上高に統計的に有意な差がある」と述べることができます。

 
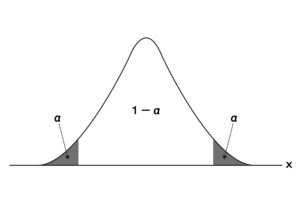
なお、t検定は両側検定と片側検定の両方で実施することができます。
上記の例は両側検定になり、「2つの群の平均値に差があるかどうか」という風に、どちらの群の売上高が高いか低いかといった方向性を特定せずに検証しています。

一方、片側検定の場合は「一方の群の平均値が他方より大きい（または小さい）かどうか」を検証します。
上記の例で考えると、「SNSの投稿量が多い群の方が売上高が高いかどうか」を調べるのであれば片側検定になります。

ただし、片側検定と限定して検討すると、「実は投稿量が少ない方が売上高が高くなる」といった予想外の結果を見落とす可能性が生じるので注意が必要です。
研究の目的や仮説に応じて、両側検定と片側検定のどちらか適切な方法を選択します。