カイ二乗検定

カイ二乗検定の定義

カイ二乗検定は、質的データの分析に用いられます。
帰無仮説が正しいと仮定したときに、検定統計量が近似的にカイ二乗分布に従うことを利用した検定法の総称です。

この検定法は、質的データを扱うことや、仮説のもとでの期待度数の算出に関して正規分布に基づく仮定が少ないことなどから、一般的にノンパラメトリック検定に分類されます。

 
カイ二乗検定は適合度の検定や、２つの質的変数の独立性の検定などに、主に用いられます。

適合度検定は、観測されたデータが理論的な分布にどれだけ適合しているかを評価します。
具体的には、観測値と理論的な期待値がどれだけ乖離しているかを表すカイ二乗統計量を計算して、その値が小さいほどデータと期待値との適合がよいと判断されます。

独立性の検定は、2つのカテゴリカル変数が独立であるかどうかを判断します。クロス集計表を用いて観測された値と、理論的な期待値の乖離からカイ二乗統計量を計算し、帰無仮説を評価します。

適合度検定はデータが特定の分布に従うかどうかを確認するために使用され、独立性の検定は異なる変数間の関係性を調べるために使用されます。

カイ二乗検定の補足ポイント

適合度とは、統計モデルや確率分布が観測されたデータにどの程度当てはまっているかを、何らかの側面から評価する指標のことです。

カイ二乗検定の場合は、実際に観測されたデータである実測値と、理論的に期待されるデータである期待値との差異から、適合度の検定を行うことができます。

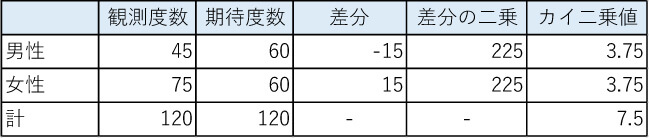
ある大学の今年の卒業者のうち、卒業後に教員を志望した学生の男女比を調べたとします。
教員を志望した120名のうち、期待される男女比は1：1の男性60人、女性60人と仮定したところ、実際に調査すると男性45人、女性75人でした。

ここでは数式の解説は省略しますが、手順としては、まず期待確率と期待度数を算出します。

男女比は半々を想定するのであれば、期待確率は50%になります。
調査対象者120人の50%ということは、期待度数は60人です。

次に、観測度数と期待度数の差の二乗を期待度数で割った値の和を計算して、カイ二乗値を算出します。

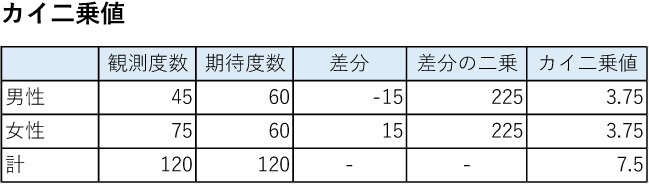
まず男性から計算すると、観測度数は45、期待度数は60であり、観測度数と期待度数の差は-15、その二乗は225です。
したがって、225を60で割った3.75がカイ二乗値となります。

同じように計算すると、女性についても3.75というカイ二乗値が得られるので、男女あわせて7.5が合計のカイ二乗値です。

また、自由度という数値も計算しますが、これは検定で扱うカテゴリー数から１を引いた数です。
男性と女性という２つのカテゴリーがあるので、自由度は１ということです。

そして、カイ二乗分布表というものを参照して、自由度が１、今回は有意水準1%と設定して臨界値を参照してみると、6.63ということがわかります。
カイ二乗分布表もここでは割愛していますが、多くの統計学のテキストに巻末の表として添付されています。

カイ二乗値がこの臨界値を上回ると、得られた結果は統計的に有意だと判断されます。

今回の例では、カイ二乗値は7.5であり、臨界値6.63を上回っているため、調査対象となった教員志望の学生の男女比は、有意に女性の数が多かったと考えることができます。

MEMO

カイ二乗検定の中では、今回取り上げた適合度の検定の他に、独立性の検定もよく使用されます。
独立性の検定の適用例としては、希望する職種と性別との間に関係があるかを調べる場合などが考えられます。
例えば、「希望職種」と「性別」という２つの質的変数について質問紙調査をして、下記のようなクロス集計表として整理します。

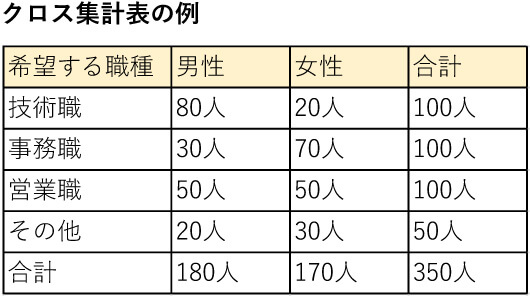
そして、「希望職種」と「性別」は独立である、つまり両者の間に関連はないという帰無仮説を立てたとしたら、その仮説が支持されるか、棄却されるかを判断します。