有意差の定義
有意差とは、2つの測定値の間に見られる差が、「偶然ではなく意味のある、本質的な差」として一般化できることを示す概念です。
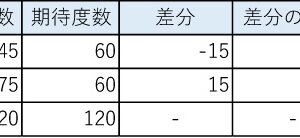
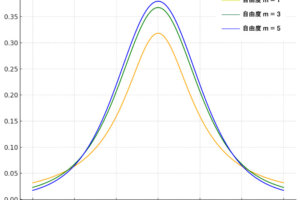
有意差があるかどうか判断するためには「t検定」「分散分析」「カイ二乗検定」などといった統計的検定が用いられます。
「~には有意差がある」と考えるのが一般的な研究仮説ですが、通常、統計的検定の手続きでは、研究仮説とは逆の「~には有意差がない」という仮説を立てます。これを帰無仮説と言います。
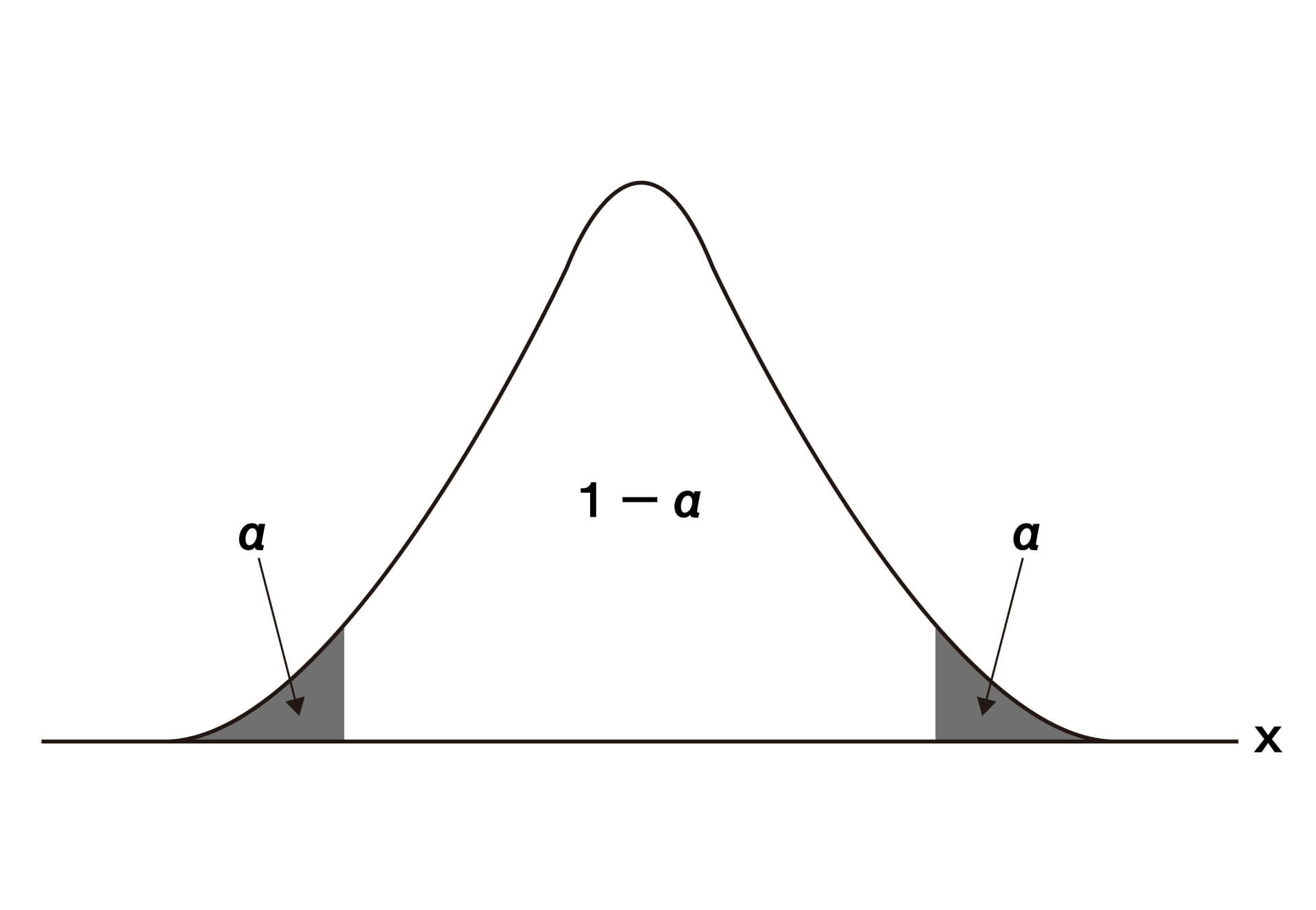
この「有意差はない」とする帰無仮説が偶然に正しいとされてしまうことが、1~5%の水準以下の確率でしか生じないと示されれば、この帰無仮説は棄却されます。
帰無仮説の方が正しいとする、この1~5%という確率は、有意差を左右する水準であることから有意水準と呼ばれます。
帰無仮説を棄却するということは、研究仮説が採択されるということになり、結果、それらの間には「有意差がある」という推定がなされることになるのです。
有意差の関連キーワード
- 研究仮説
- 帰無仮説
- 有意水準
- 第一種の誤り
- 第二種の誤り
有意差の補足ポイント
「有意差なし」という結果が得られたからといって、「AとBには差がない」つまり「AとBが完全に等しい」ということを実証したことにはならないのが、統計的検定の難しいところです。
統計的検定における「有意差なし」とは、2条件の差を「偶然起こりうる程度の差」と見なし、「統計的に意味のある差ではない」という判断を下したに過ぎないのです。
したがって、統計的検定では、研究仮説である「差がある」ということを実証することはあっても、条件差がまったく存在しないということ、つまり完全に等しいということを示すのは、まず不可能なわけです。
ここで、有意差の関連事項として「第一種の誤り」「第二種の誤り」についても確認しておきましょう。
本当は帰無仮説が正しい、つまり有意差がないにもかかわらず、誤って帰無仮説を棄却してしまい、有意差があると判断してしまう危険性を第一種の誤りと言います。
一方、本当は帰無仮説が間違っている、つまり、有意差があるにもかかわらず、誤って帰無仮説を採択し、有意差はないと判断してしまう危険性を第二種の誤りと言います。
第二種の誤りは、データに含まれる貴重な情報の見落としという意味で、できるだけ避けたいものです。
しかし、より注意しなければならないのは第一種の誤りとされています。
なぜなら、本来まったく関係のないものに、関係性を持たせてしまうことになるからです。
第一種の誤りは、有意水準と同じ確率となるため、有意水準が高ければ高いほど、危険性も増すということになります。
これらはほんの一例ですが、統計的検定は完璧なものではなく、ところどころに落とし穴があるということが分かりますね。
検定結果がすべてと考えるのではなく、データの大きさの確認や、信頼区間などといったその他の推定を参考にすることが大切なのです。
有意差の有無だけで議論を完結させるのではなく、「その差に実用的な意味があるか(臨床的意義)」を考える視点も重要です。
特に心理学の分野では、わずかな差でも現場での影響は大きいことがあります。
統計的有意性と実用的有意性は別物であることを意識し、結果を現実の文脈でどう解釈し活用するかが問われます。